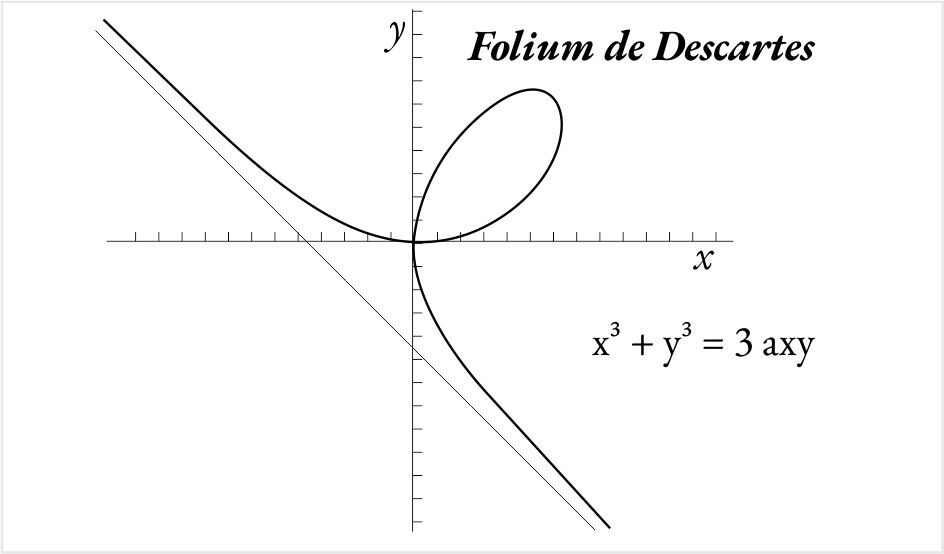
A geometria analítica é uma divisão da matemática que descreve com letras e símbolos as figuras geométricas, suas características, correlações ou propriedades. A lua cheia desenha nos céus um círculo exato, e a geometria analítica o descreve usando a expressão x² + y² = r². Os matemáticos, ao verem tal expressão, sabem que ela está noticiando ou descrevendo um círculo ou circunferência. Fermat pesquisou o conhecimento acumulado de grandes analistas como Diofante, Euclides, Arquimedes e Pitágoras sobre a teoria dos números. As observações, problemas e soluções relacionados ao Teorema de Pitágoras sugeriram a ele que Euclides havia compilado extenso número de ternas pitagóricas e sondado possíveis soluções para seu famoso último teorema. Seu trabalho desperta interesse generalizado, atrai a atenção de dedicados pesquisadores e envolve brilhantes cientistas nos estudos lógicos e abstratos acerca da teoria dos números, dos espaços e medidas da geometria, de identificação de padrões naturais.

Maria Gaetana Agnesi foi uma linguista, teóloga, benfeitora, filósofa e matemática italiana, reconhecida como tendo escrito o primeiro livro que tratou, simultaneamente, do cálculo diferencial e integral. Ela, também, se tornou fluente em diversas línguas tais como francês, latim, grego, hebraico, dentre outras.

Em 1739, seu pai não permitiu que ela ingressasse num convento de freiras. Porém, ele a autorizou a usar vestimentas simples, ir à igreja quando desejasse e liberou-a da obrigação de frequentar eventos sociais da nobreza. Maria Agnesi concentrou estudos na área da matemática publicando sua principal obra intitulada “Instituzioni analitiche ad uso della gioventu italiana” (Fundamentos analíticos para o uso da juventude italiana), que versa sobre álgebra, trigonometria, geometria analítica, cálculo e equações diferenciais. Seu trabalho revolveu o mundo acadêmico científico ao reunir as ideias de Isaac Newton e Gottfried Leibniz, com análise de quantidades finitas e infinitas, e por ordenar as descobertas do século XVII com clareza, permitindo aos estudantes o acesso à pesquisa matemática consolidada.

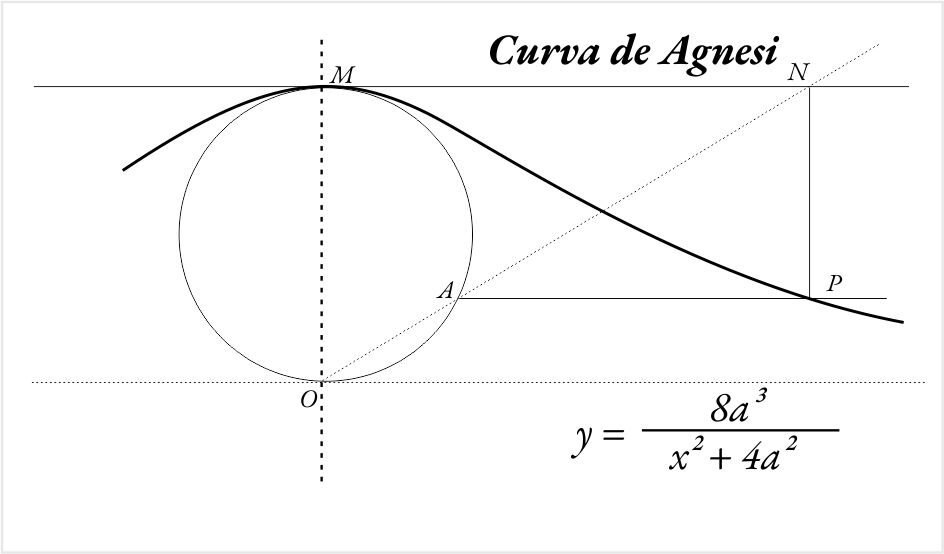
É destaque em sua obra o estudo de uma curva originalmente analisada por Pierre de Fermat (1639) e por Guido Grandi (1703), denominada “versiera” – termo latino significando virar –, que é expressa pela equação x²y + a²(y – a) = 0, com a > 0, definida matematicamente por Gaetana, e é comumente conhecida como “Curva de Agnesi” ou “Bruxa de Agnesi”. O matemático Grandi, anteriormente, havia denominado a curva de Scala. Agnesi dedicou seu livro à Imperatriz Maria Teresa da Áustria, recebendo de presente uma caixa de cristal com brilhantes e um esplêndido anel de diamante. O Papa Bento XIV a presenteou com uma coroa de ouro e a nomeou professora honorária da faculdade de Bolonha em outubro de 1750, para ocupar a cadeira de matemática e filosofia natural.

Guido Grandi foi referenciado por Bento XVI, em 2012, Papa Emérito, em homília dirigida à Ordem Camaldulense nos seguintes termos: “(…) Graças à fidelidade e à benevolência do Senhor, a Congregação dos Monges Camaldulenses da Ordem de São Bento pôde percorrer mil anos de história, alimentando-se quotidianamente da Palavra de Deus e da Eucaristia, tal como tinha ensinado o fundador São Romualdo, segundo o «triplex bonum» da solidão, da vida em comum e da evangelização. Figuras exemplares de homens e mulheres de Deus, como São Pier Damiani, Graziano – o autor do Decretum (…); homens de ciência e de arte como Frei Mauro (…) Pietro Delfino e Guido Grandi; historiadores ilustres (…) zelosos Pastores da Igreja, entre os quais sobressai o Papa Gregório XVI, mostraram os horizontes e a grande fecundidade da tradição camaldulense (…).”

Em 19 de março de 1752 com a morte de seu pai, Maria Gaetana abandonou suas preocupações acadêmicas. A partir desta data ela dedicou sua vida ao estudo da teologia, às Sagradas Escrituras e às atividades de caridade com pessoas necessitadas. Em 1759 Agnesi alugou uma casa e a transformou em um abrigo para pobres, doentes, desabrigados e deficientes mentais, obtendo os recursos para realizar seu projeto através da venda dos presentes recebidos por seus trabalhos anteriores.

Fermat, entre outras realizações científicas, consolidou o uso dos eixos perpendiculares e da base de coordenadas ortogonais, propôs e demonstrou inúmeros teoremas, enunciou uma propriedade fundamental da luz afirmando que ela sempre segue o caminho mais curto, ou mais breve, possível. Este princípio estabelecido por Fermat e que atualmente é uma das propriedades mais básicas da ótica, não foi bem recebido pelos estudiosos e filósofos de sua época. Seus estudos e seu trabalho produziram os instrumentos técnicos que permitiram as incursões científicas de Grandi, de Maria Agnesi e de Isaac Newton, assim como ensejaram inúmeras proposições de outros talentosos, verdadeiros e honrados cientistas.

Guido Grandi era padre, monge beneditino da Congregação dos Monges Camaldoleses, professor de filosofia, teologia e matemática. Durante viagem à Inglaterra em 1709, Guido foi eleito membro da Royal Society por cientistas locais, tendo seu nome sido indicado por Isaac Newton para ocupar este distinto cargo. Em 1714 Grandi tornou-se professor de matemática na Universidade de Pisa.

Em 1783 Agnesi se mudou para o instituto Pio Trivulzio, dedicou o restante de sua vida a gerenciá-lo continuando a prestar seus cuidados para as pessoas carentes ou necessitadas. A 9 de janeiro de 1799, com oitenta e um anos, Agnesi faleceu e foi sepultada nos arredores de Roma, numa campa com quinze idosos pobres, sem qualquer monumento sobre seu sepulcro. No centenário de seu falecimento, Maria Gaetana foi homenageada na cidade de Milão com a nomeação de ruas e uma escola.

Fermat morreu em Castres em 12 de janeiro de 1665, depois de receber os sacramentos, mantendo-se sempre lúcido. Ele foi enterrado no dia seguinte, na presença de todos os magistrados católicos do parlamento, na capela católica em Castres. Em 1675 seus restos mortais foram transferidos e enterrados na igreja do Convento Agostiniano em Toulouse. Em 1793 a Revolução Francesa e seu iluminismo ilustre, destruiu o túmulo de Pierre de Fermat, profanou seus restos mortais e os dispersou de modo a não permitir sua localização e a recomposição de sua sepultura.

Especialmente, Monsieur Pierre reafirmou e comprovou que, ao contrário do que muitos pensam e definem, as verdades matemáticas nem sempre são descobertas por dedução. As provas podem, de fato, ser deduzidas e podemos com naturalidade expressar matematicamente as mais diversas conjecturas e fantasiosas propriedades de universos que não existem na realidade. Podemos transcrever matematicamente todas as quimeras, devaneios e caprichos que nossa imaginação esteja disposta a criar. Porém, mais adequadamente, as descobertas podem surgir pelo reconhecimento de um padrão advindo da realidade, capaz de originar conjecturas e proposições tais que, se provadas, transformam-se em referências científicas. Estas descobertas resultam da observação consistente da Realidade que nos cerca, que nos impõe suas verdades inalteráveis  às quais conhecemos e sob sua regência convivemos. Isto se aplica com absoluta propriedade para a solução maravilhosa do milenar “Último Teorema de Fermat”, confirmando que levantar conjecturas a partir da identificação de um padrão é perfeitamente legítimo, com muitos teoremas sendo assim construídos. É preciso, naturalmente, tomar cuidados especiais para não produzirmos afirmações matemáticas precipitadas, seja para negar, seja para chancelar uma hipótese.

O Tomo IV e o Tomo V do “A Origem do Bem e do Mal – O Último Teorema de Fermat” tem mais informações a respeito de Fermat, sua piedosa devoção Católica Apostólica, seu teorema e a maravilhosa solução que ele disse que haveria de existir.